Time-Series Regression on Android

Regression is an analytic technique used in developing predictive models for numerical data. It automatically derives mathematical functions that summarize trends embedded in past historical data, in such a way that minimizes the errors between actual input data and predicted values by the models. Regression can be applied to time-series data. A time-series consists of a set of observations which are measured at specific time intervals, say, monthly, quarterly, yearly, etc. The following figures show MyDataSay Android Time-Series Models. Enter time-series data and click the "Evaluate" button. Then result will show as in the right figure.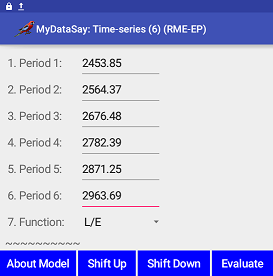

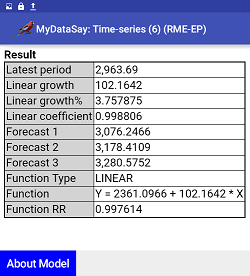
Linear Growth and Linear Growth Percent

Linear growth numbers can be best understood with linear time-series regression. Linear regression formula is stated as "Y = a + b * X" where "b" is the periodic average increase/decrease amount. "b" is the "Linear growth" in the following figure. This is the exact linear average growth amount. This method of growth computation is best for linear growth data. If data is not linear, this should be used with caution. "Linear growth %" is the percentage ratio of the "b" value over the average of input series data. This computation method is complex. But it provides "precise" linear growth amount and percentage ratio. You can use the MyDataSay models to compute this.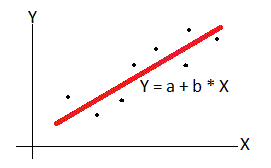

Current MyDataSay download supports the following models;

• Time-series regression up to 6 periods with moving average smoothing.
• Time-series regression up to 12 periods with moving average smoothing.
• Time-series regression up to 50 periods with seasonal adjustment.
• Regression up to 20 "X-Y" pairs.

To download the models, click MyDataSay Download. It's a .zip file. Read the "USER-INSTALL-GUIDE.txt" for installation on your Android devices. Android 3.0.0 or newer versions are supported. After importing models, time-series models will be available from "Time Series Models".